Robust Tracking and McNair Research Conference Demonstration

It has been a while since I have posted any progress on Project PAALM. However, I have been working on numerous aspects the framework and a demonstration video. 

In my last update, I described having uncovered a way to map end-effector positions for the index finger.  Since then, I have implemented mapping for all fingers and the thumb, and integrated Autodesk Maya's Inverse Kinematics (IK) Handle tool to solve for optimal joint angles. Originally, I was using my own implementation of Cyclic Coordinate Descent but the approach was resulting in delayed visual feedback while passing the data through the web socket. The IK Handle tool is optimized and can solve for joint angles almost instantaneously from within Maya.  

Previously, the framework would disregard any translation of the palm resulting in only animated finger movements. I recently updated the framework to include palm tracking so that hand animations respect the input provided by a user.

On Saturday, September 21, 2013, I had the pleasure of presenting my research at the University of Maryland, Baltimore County, 21st Annual McNair Research Conference. The feedback I received was astounding and is pushing me to delve deeper into my endeavor.

From Left to Right: Dr. Robert Lane (Director of the Pre-Doctoral Initiative at the University of Pennsylvania), two other UPenn presenters, and myself on the right

Joint Angle Estimation for the Index Finger

Earlier today I implemented a way to map end-effector positions of the index finger from the Leap Motion controller to a target point visualized as a unit-radius sphere in Maya. Each frame update from the Leap Motion controller is first processed for the presence of fingers. If fingers exist, the fingers are sorted by their x-coordinate values. This facilitates selecting the index finger using index position '1' (the thumb lies in position '0', the pinky in position '4', etc.). Using this indexed array, we isolate the index finger, take its tip position and subtract the Leap's detected palm position from this value. The result gives us the direction vector of the index finger. 

The direction vector is useful for a number of reason. First, it describes the way the finger is positioned relative to the palm in space. Second, its length gives us information about the bend of the finger. We consider the length of the finger with an open, flat palm (all fingers extended) to be our base length. In every frame, we can use the current length of the direction vector to determine a target position for the  sphere in Maya. The smaller the length of the direction vector, the more likely the finger is to be bent. 

With this length aspect in mind, I devised a way to get a base length of the index finger. This is the length that will serve as the means of comparing all subsequent lengths from direction vectors. The purpose of the comparison will will become clearer in a moment. Calculating the base length is simple a process that samples the first 1000 frames in which fingers are present, determines their direction vectors, computes their lengths and average all of the values for each individual finger.  After the average length is calculated, the process of relaying position updates to Maya remains the same; however, there is one additional piece of information. We now send along lengthRatio, the ratio of the finger's length in the current frame to the base length. 

In Maya, we maintain the length of the joint chain (this can be calculated at run time if need be). When we receive a position update from the Leap with the direction vector and a lengthRatio, we normalize the direction vector and multiply it by the product of joint chain length and the lengthRatio.  We now need to obtain the position of the target point relative to the base of the joint chain using this direction vector. This is accomplished by adding the position of the joint chain base to the direction vector. The result is now a target positon mapped from the Leap coordinate space to Maya coordinate space with respect to the joint chain. We apply a translation transformation to the target point sphere using the  (xform) command. This then triggers a function call to perform Cyclic Coordinate Descent for estimating the joint bend angles. 

The reasoning behind using the lengthRatio, is simply to allow us to map a wider range of motion into Maya. Applying only the joint chain length to the unit direction vector tells us nothing about how a finger is actually bent. In fact, its sole application keeps the position of the target point on the surface of a sphere with a radius equal to the joint chain length and base at the joint chain base. The lengthRatio, on the contrary, describes how the target point sphere should be positioned on the joint chain sphere's surface (ratio equal to 1) or inside of the sphere (ratio is less than 1). 

One potential issue with this method is that the sampling/averaging process is (of course) not an exact measurement. Namely, if the user loosens their hand in the initial sampling process, the average length will be smaller than it should be. When the user decides to fully extend their fingers and open their palm during normal frame updates, the ratio will be greater than 1 causing positioning of the target point to be out of reach with respect to the joint chain length. This is a minor issue- we easily handle this occurrence using a projection procedure. If the position of a target point lies outside of the reach of the joint chain, we project that point onto its respective location on the surface of a sphere that has a radius equal to the joint chain length and a center at the base of the joint chain.

Cyclic Coordinate Descent & Forcing Maya UI Updates

Previously, I described my plan to implement an algorithm called Cyclic Coordinate Descent (CCD) and integrate it into Maya. The process was cumbersome, but I am happy to report that my attempt was successful. 

The largest source of trouble originated from understanding Maya's construction of composite matrices for object transformations and the various application programming interfaces for data types like Matrices and Quaternions. Initially, I went the route of using the Leap Motion SDK data types (Leap Vectors, Matrices, etc) to calculate the rotation angles for a joint while performing CCD. However, problems arose when I attempted to translate Maya's composite matrix (as an array of double values) into Leap Matrices and then back to a Maya Matrix after applying a rotation. Artifacts would result in the Leap Matrix that I could not remedy because the Leap SDK does not permit direct access to the data backing a matrix. 

After discovering the artifacts, I delved into Maya's data types but encountered more trouble because their interface for matrices has some of the same limitations that the Leap data types have- namely, direct access to matrix values is not possible. My latest (and successful) shift was to PyMel, a Python wrapper around Maya commands that adds the functionality that I needed.

With PyMel in place, the only other feat was Gimbal Lock. Gimbal Lock is an issue that results when using Euler angles for the rotation of 3D objects in space. Essentially, successive rotations can result in two rotation axes locking in the same plane. Subsequent rotations about these locked axes causes a single rotation to applied to the object with respect to that plane. Effectively, the object loses a rotational degree of freedom.

On the left, you see how each gimbal allows rotation around 

a specific axis. On the right, you can see a set of gimbals in 

gimbal lock. The inner-most gimbal can't change in pitch 

unless the gimbals are put into another positions. 

[Source: HowStuffWorks]

There are a number of ways to avoid Gimbal Lock such changing the order of rotation about axes after detecting when a sequence of rotations is likely to cause Gimbal Lock. I decided to use axis-angle rotation pairs and convert those into quaternions. There are two benefits to using this approach. The first is obviously that quaternions avoid Gimbal Lock;  they permit rotations to occur about an arbitrary axis in space. The second benefit (though not currently in use), is that they permit 3D rotation to be animated smoothly (Spherical Linear Interpolation).

As a secondary update, I have changed the way in which the Leap Motion controller interfaces with Maya. Originally, a listener object would compute position and rotation updates then send them in Maya Embedded Language (MEL) as a string over a socket command port linked to Maya. This implementation meant that I was performing CCD from within the Python script running in my Bash. Thus, references of the rotation and positions of joints had to be queried each time a transformation on a particular joint in the chain occurred. The logic behind this rests in the fact that an arbitrary rotation on a single joint node in a chain causes the positions of all connected children joints nodes to rotate as well; this propagation is a feature of the structure of a Scene Graph. 

My currently implementation places all CCD and any operations for joint transformations within the Maya python script. The Leap controller listener is only sending coordinates of end-effector positions to Maya as a string. Queries, since they are now occurring within Maya and not over a socket connection, are much faster.

A few posts back I also described an issue in the Maya UI halting on position updates. I have now found a way to solve this problem- Maya has a command called refresh permits the input of a force boolean. When force is true, the command triggers a complete update of the camera views displaying the objects in a scene. I am currently using this to visualize intermediate stages of the CCD algorithm.

References
1) Cyclic Coordinate Descent (CCD)
2) PyMel - Python-Maya Wrapper Application Programming Interface
3) YouTube: Gimbal Lock
4) How Stuff Works (Image): Gimbal Lock
4) Wikipedia: Euler angles
5) Wikipedia: Quaternions
6) Wikipedia: Spherical Linear Interpolation (Slerp)
7) Maya Embedded Language (MEL)
8) Wikipedia: Scene Graph
9) PyMel API - Refresh Command

Alpha Review Recap

This is a brief update that I will follow-up with later on this weekend.

Alpha reviews occurred right before Spring Break last week. The feedback I received was very positive and helpful in moving forward. The steps I am currently taking  are implementing Cyclic Coordinate Descent attached to a time node in Maya. This will allow iterations of CCD to be slowly visualized in Maya to permit testing whether my current implementation works properly.

Until now, I have not been able to directly test my method's efficacy using the Leap because of the large amount of rapid frame updates that continually update position in Maya. I plan to have a working time node set up in Maya by the end of this weekend. Once this is completed I will update with more details.

Live Position Updates in Maya through the Leap Motion Controller

I postponed updating my research last week because I was not able to make progress in my implementation. This update, however, serves to highlight the results I have obtained solely during this weekend. 

My work has been on two components-the first involves using the Python Leap SDK to filter frame data to isolate a particular finger, and then using that finger data to obtain motion information (specifically, the end tip position of an effector after a motion); the second is integrating my data into Maya to update finger positions in real time.

Leap Motion Controller Coordinate System

I managed to implement a quick filtering algorithm that does basic sorting of fingers by x-position (relative to the Leap's coordinate system). In this manner, it is possible to order the fingers on the hand such that we can easily determine each of them. I selected the index finger as my finger of focus for this preliminary implementation. After obtaining the index finger information, I used the direction vector of motion to determine the finger's positioning in relation to the base of the finger. From the Leap perspective, the palm position was used as the base position. When mapping this information into Maya, the base position is taken to be the knuckle position.

Initially, I wrote my program in the style of a Maya plug-in using the Maya Python API. The idea was that it would be portable, effective, and fully integrated. I soon uncovered that this implementation had terrible performance effects. To elaborate, the Python Leap Motion SDK features a base class that permits a Python program to listen for 'frame' events. On a new frame capture from the Leap Motion controller, a function can be called to handle the frame data (this is where I integrated my filtering and sorting algorithm). Actual capturing of the frame data runs on a thread that only terminates after user input.

When running my script in Maya, the rapid data capture coupled with the waiting for a user input process halted the user interface (including the script editor). This is the result of scripts in the Maya running on the Main thread). When I terminated program through user input, all of the captured Leap data popped off the program call stack. Each command was then processed, but the finger tip position only snapped to the finger tip position of the most recent frame. More specifically, this was not real time and was not animated.  

I approached the problem by attempting to launch multiple threads for the processes in Maya and using different means of obtaining user input. Each attempt only resulted in Maya crashing or a complete UI halt. With the help of a friend, who found this resource for opening socket connections in Maya, I was able to open a command port, and use my Python program from within a bash (Terminal in OS X). 

The features of this approach are:

1. The open-socket permits commands to be run continuously without halting the UI in Maya. 
2. There is no need to install python modules/packages
3. Any version of Python can be used from the Bash. Likewise there are no limitations to what modules you use in the Bash. This is unlike the Maya version of Python that limits the use of modules and their functionality.

To demonstrate my progress, I have included a video showing the live updating of a finger joint position in Maya. The left pane is the Maya Editor window. The top-right pane is the Maya Script Editor. The bottom right pane is the Bash window that has my Python program running. It currently prints out the effector tip position for each frame capture.

My next goal is to implement the Cyclic Coordinate Descent algorithm to perform inverse kinematics and estimate the phalangeal joint angles.

Project PAALM - It's Official

I have officially submitted my preliminary proposal for Project PAALM. I am very excited to start building my prototype! My proposal is available here: Project PAALM Proposal.

Testing the Functionality

In an effort to understand the information obtainable through the Leap Motion controller, I tested out the functionality using the Software Development Kit's (SDK) visualization program. It provides a decent interface for understanding and visually showing information the controller is receiving. Before I talk about what sort of information I am able to receive, it is probably useful to discuss some basic information about the structure of the hand and its phalanges (fingers):

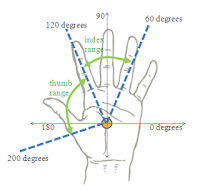Phalangeal Range of Motion

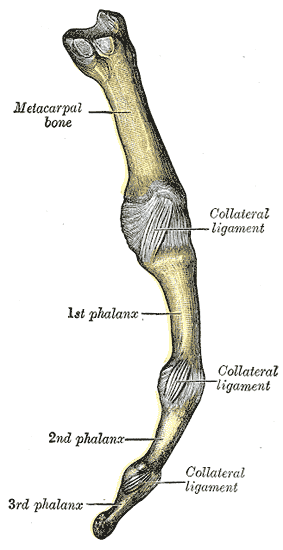The Finger Structure

The hand has a very complex structure permitting a wide range of motion to each of its appendages. Additionally, each finger has its own motional complexity. The finger can divided into three phalanges bones that are connected by collateral ligaments. Ligaments are the tissues that connect bones to other bones. In the case of the finger, they provide the mechanism of joints. As an example, in the figure on the left, the collateral ligament between the metacarpal bone and the 1st phalanx forms what is typically called the 'knuckle'.

From the finger structure, there exist three possible joints that theoretically can be independently moved. This is the case for all of the fingers. The thumb, however, only has a knuckle joint and one additional joint connecting its two phalanges. That is not to say that the thumb is less complex. Its opposability gives it a much larger range of motion and thereby greater complexity.

Returning to the Leap- I used their visualization that depicts effectors as cylinders. The basic method displays them as vectors in 3D space, but that is not as helpful when analyzing movements relative to each finger. The cylindrical representation also makes it easier to see relative lengths of the fingers (widths, unfortunately, do not currently reflect the actual widths of the fingers). 

There is a good amount of information that can be visualized (as well as received in terms of data from the Leap). In particular, it is possible to see the palm normal of the hand. When moving the separate fingers, this information is useful because we can tell how fingers can move relative to a (presumably) stationary plane. Angle calculations, at the very least, can be made with respect to the knuckles. 

Palm Normal

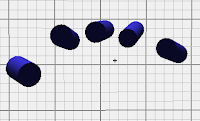Fingers Visualized as Cylinders

There is an interesting problem to solve in terms of how the direction of the effector (the finger vector) can be used to achieve the joint angles present along the other two bend angles on each of the fingers (and the one angle of the thumb). 

To begin, I will most likely assume that the joint angle move in sync. This assumption will allow me to interpolate bend angles along the finger to at least get a working prototype. From there, I will attempt to find a mechanism for achieving better estimates of all of the joint angles. This may result in the use of multiple Leap devices to capture information from different view angles.

Another bit of information that is potentially useful in detecting joint angles is the palm sphere radius. This works by estimating the radius of a spherical object that could be held by the hand. A closed hand produces a smaller sphere radius while a large one produces a larger radius. This information is useful because a smaller radius implies a closed hand, thereby the fingers must be angled downward. I'm not sure how this can be used for joint angles, but that is something I will find out.  I will end here with some goals for this week:

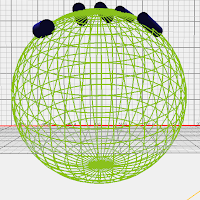Open Palm

Closed Palm

1. Finish my proposal for Project PAALM.
2. Start reading through the research on hand motion detection devices and hand tracking.
3. Start working on a prototype that will at least give some information about estimated joint angles. I will work towards just visualizing and estimating angles for a single finger (probably the index).